MECÂNICA GENERALIZADA GRACELI - QUÂNTICA QUÍMICA RELATIVISTA [14]

EQUAÇÃO DE ONDAS DE GRACELI.

G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

G = OPERADOR DE GRACELI EM ESTADOS QUÂNTICOS QUÍMICO RELATIVÍSTICOS.

E = ENERGIA DO SISTEMA DOS ESTADOS E SEUS POTENCIAIS DE INTERAÇÕES DE CAMPOS E ENERGIAS E TRANSFORMAÇÕES.

ψ = função de ondas.

μ = potencial químico.

h = constante de Planck.

c = velocidade da luz.

[ξ ]= interações das forças fundamentais = eletromagnética, forte e fraca.

[,ς] = valência, distribuição eletrônica, níveis e subníveis de energia, estado molecular e de interações entre partículas, potencial químico dos elementos químicos, potencial de interações e transformações entre campos e partículas, potencial de transformações de elétrons, átomo, e elementos químicos, e outros.

EQUAÇÃO DE ONDAS DE GRACELI.

G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

G = OPERADOR DE GRACELI EM ESTADOS QUÂNTICOS QUÍMICO RELATIVÍSTICOS.

E = ENERGIA DO SISTEMA DOS ESTADOS E SEUS POTENCIAIS DE INTERAÇÕES DE CAMPOS E ENERGIAS E TRANSFORMAÇÕES.

ψ = função de ondas.

μ = potencial químico.

h = constante de Planck.

c = velocidade da luz.

[ξ ]= interações das forças fundamentais = eletromagnética, forte e fraca.

EQUIVALÊNCIA GRACELI ONDAS - ENERGIA.

G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

ESTATÍSTICA GRACELI.

1 / G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c [-1] .

em que $g_{s}$ é a degenerescência quântica do estado $s$ , $\epsilon _{s}$ é a energia do estado $s$ , $\mu$ é o potencial químico, e $\beta =1/k_{B}T$ , em que $k_{B}$ é a constante de Boltzmann[1]

EQUIVALÊNCIA MOMENTUM = ONDAS.

MO = G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

EQUIVALÊNCIA

MASSA = ONDAS.

COMPRIMENTO = ONDAS.

ENERGIA = ONDAS.

E = M=COMPRIM. = G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

[Ϡ ] = DENSIDADE DE ESTADOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS NORMAIS E DE PLASMAS E ESTADO CONDENSADO, ESTADO DE DISTRIBUIÇÃO ELETRÔNICA E NÍVEIS DE ENERGIA, ESTADO MOLECULAR E ESTRUTURAL, DE LIGAMENTOS E INTERAÇÕES DE CAMPOS E ENERGIAS, DE POTENCIAL QUÍMICO, DE TRANFORMAÇÕES, DE ENERGIA DE LIGAÇÃO, DE POTENCIAL DE FUSÃO, POTENCIAL DE SOLIDIFICAÇÃO, E OUTROS, COMO OS DAS DEZ DIMENSÕES DE GRACELI.

Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.

Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.

De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.

E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.

E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.

Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia.

Explanação

Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia.

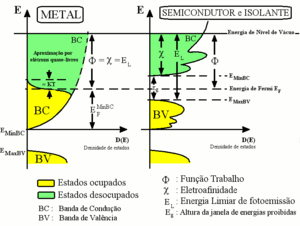
Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos $E_{g}$ de energia de maneira a realizarem a transição a outro estado disponível.

A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, $\rho$ , n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE.

Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é

E={\frac {(\hbar k)^{2}}{2m}}

E para fótons, a fórmula é

E=\hbar ck

Pode também ser escrito como uma função da frequência angular $\omega$ , a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação.

Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é

G(k)\,dk={\frac {nV}{2\pi ^{2}}}\,k^{2}\,dk,

onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons.

Materiais cristalinos

Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade.

Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário $V=L^{3}$ , somente vetores k são mantidos satisfazendo

(k_{x},k_{y},k_{z})={\frac {2\pi }{L}}(n_{x},n_{y},n_{z}),

onde $n_{i}$ são inteiros positivos ou negativos arbitrários. Usando

|k|^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2},

pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é

G(k)={\frac {Vk^{2}}{2\pi ^{2}}}

para um único caso.

Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é

g(E)=G(k(E)){\frac {dk}{dE}}.

A relação acima é somente significativa se a energia somente depende da manitude $|k|$ do vetor k.

EQUAÇÃO DE ONDAS DE GRACELI.

G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

G = OPERADOR DE GRACELI EM ESTADOS QUÂNTICOS QUÍMICO RELATIVÍSTICOS.

E = ENERGIA DO SISTEMA DOS ESTADOS E SEUS POTENCIAIS DE INTERAÇÕES DE CAMPOS E ENERGIAS E TRANSFORMAÇÕES.

ψ = função de ondas.

μ = potencial químico.

h = constante de Planck.

c = velocidade da luz.

[ξ ]= interações das forças fundamentais = eletromagnética, forte e fraca.

A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação EF, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Introdução

Contexto geral

Esta seção não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: Google (notícias, livros e acadêmico) (Julho de 2022)

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

\mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]

onde εF é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica é da ordem de 105K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo ENtotal a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e EN-1total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

EF = ENtotal - EN-1total

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de $E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}$ , ou duas partículas podem ter energia $E_{2}=4E_{1}$ e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos nx, ny, e nz. As energias da partícula isolada são

E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,

nx, ny, nz são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo $E_{100}=E_{010}=E_{001}$ . Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\vec {n}}=\{n_{x},n_{y},n_{z}\}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,

O número de estados com energia menor que Ef é igual ao número de estados que residem em uma esfera de raio $|{\vec {n}}_{f}|$ na região do "n-espaço" onde nx, ny, nz são positivos. No estado básico este número iguala o número de férmions no sistema.

N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}

então a energia de Fermi é dada por

E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}

={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L2 com V2/3):

E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,

A energia de Fermi total de um esfera de fermi de $N_{0}$ férmions é dada por

E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}

E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN

={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}

Energia de Fermi total:

E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}

Integração por substituição:

E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}

E_{t}={\frac {3}{5}}N_{0}E_{f}

A eliminação de $L$ em favor de $V$ :

L^{2}=V^{\frac {2}{3}}

E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 1036 elétrons/m3. Isto significa que sua energia de Fermi é:

E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.[2]

O raio do núcleo é aproximadamente[3]:

R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV}

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.

EQUIVALÊNCIA GRACELI ONDAS - ENERGIA.

G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

ESTATÍSTICA GRACELI.

1 / G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c [-1] .

EQUIVALÊNCIA MOMENTUM = ONDAS.

MO = G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

EQUIVALÊNCIA

MASSA = ONDAS.

COMPRIMENTO = ONDAS.

ENERGIA = ONDAS.

E = M=COMPRIM. = G ψ = E ψ = [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ψ μ / h/c .

Explanação

Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é

E={\frac {(\hbar k)^{2}}{2m}}

E para fótons, a fórmula é

E=\hbar ck

Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é

G(k)\,dk={\frac {nV}{2\pi ^{2}}}\,k^{2}\,dk,

Materiais cristalinos

(k_{x},k_{y},k_{z})={\frac {2\pi }{L}}(n_{x},n_{y},n_{z}),

onde $n_{i}$ são inteiros positivos ou negativos arbitrários. Usando

|k|^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2},

pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é

G(k)={\frac {Vk^{2}}{2\pi ^{2}}}

para um único caso.

Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é

g(E)=G(k(E)){\frac {dk}{dE}}.

A relação acima é somente significativa se a energia somente depende da manitude $|k|$ do vetor k.

A Teoria do Funcional da Densidade (do inglês, Density Functional Theory, DFT) é uma das mais populares teorias da mecânica quântica utilizada para descrever propriedades eletrônicas na física do estado sólido, química quântica, ciência dos materiais, bioquímica, biologia, nano-sistemas e sistemas em escala atômica. Com essa teoria, as propriedades de um sistema com muitos elétrons podem ser determinadas aplicando funcionais, funções que recebem como argumento uma outra função, sobre a densidade eletrônica, o que origina o nome Teoria do Funcional da Densidade. A DFT é um dos métodos mais versáteis disponíveis em física da matéria condensada, física computacional e química computacional devido a generalidade de seus fundamentos e a flexibilidade de implementação. Os cálculos de DFT são ab initio (de primeiros princípios) não usam parâmetros experimentais ou empíricos e têm grande impacto na ciência dos materiais por seu poder preditivo com um custo computacional praticável.

Visão geral

O tratamento quântico completo de um sistema de muitos elétrons, sob um potencial externo, deve considerar a repulsão coulombiana entre cada par de elétrons e a interação de spin. Esse problema não tem solução analítica, já que a função de onda total deve depender da distância entre todos os elétrons.

O método de Hartree-Fock (1930) é uma das teorias que busca resolver esse problema utilizando a função de onda como variável fundamental e apesar de apresentar resultados precisos, envolve um alto custo computacional^[1]. Já o modelo de Thomas-Fermi (1927), desenvolvido independentemente por Llewellyn Thomas e Enrico Fermi, é considerado o precursor da DFT e também busca resolver o problema quântico de muitos corpos. Essa é a primeira teoria a propor a determinação da estrutura eletrônica em termos da densidade, invés das funções de onda individuais de cada elétron. Esse modelo só é válido no limite de uma carga nuclear infinita e usá-lo para sistemas reais produz previsões quantitativas pobres.

Com a ideia inicial de Thomas-Fermi sobre o papel essencial da densidade eletrônica, Pierre Hohenberg e Walter Kohn (1964) demonstraram que a densidade eletrônica $n(x,y,z)$ determina completamente o problema quântico e pode ser usada para resolvê-lo de forma exata. Walter Kohn recebeu o prêmio Nobel de Química em 1998 por seu desenvolvimento da Teoria do Funcional da Densidade^[2].

Após seu desenvolvimento, a DFT tem sido utilizada para cálculos em física do estado sólido e, em muitos casos, os resultados concordam satisfatoriamente com os dados experimentais e os custos computacionais são relativamente baixos quando comparados ao método de Hartree-Fock. Entretanto, a DFT não era considerada precisa o suficiente para cálculos em química quântica até a década de 1990, quando os funcionais de troca e correlação foram refinados para prover um balanço entre custo computacional e precisão dos resultados.

Apesar das melhores aproximações para os funcionais de troca e correlação, ainda existem dificuldades em usar a DFT para descrever adequadamente as interações intermoleculares, especialmente as forças de van der Waals, as excitações de transferência de cargas, estados de transição, sistemas fortemente correlacionados e em cálculos do gap de energia em semicondutores.

Formalismo

Equação de Schrödinger

A Teoria do Funcional da Densidade busca resolver a equação de Schrödinger que descreve como o estado quântico de um sistema de muitos corpos evolui com o tempo^[3]. A equação abaixo é a equação de Schrödinger dependente do tempo em 3 dimensões ( $\mathbf {r}$ é o vetor posição que, em coordenadas cartesianas, pode ser escrito como $\mathbf {r} =x{\hat {x}}+y{\hat {y}}+z{\hat {z}}$ )

$i\hbar {\frac {\partial \Psi (\mathbf {r} ,t)}{\partial t}}=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,t)$

Ao utilizar o método de separação de variáveis, obtém-se a equação de Schrödinger independente do tempo

$\left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right]\psi (\mathbf {r} )=E\psi (\mathbf {r} )$

com o termo entre colchetes sendo o hamiltoniano, $E$ os valores de energia e $\psi (\mathbf {r} )$ os autoestados do sistema independentes do tempo. Essa equação pode ser escrita como uma equação de autovalores e autovetores da forma

$H\psi (\mathbf {r} )=E\psi (\mathbf {r} )$ .

Aproximação de Born-Oppenheimer

Para a descrição quântica completa de um sistema atômico ou molecular, o hamiltoniano deve incluir tanto o movimento dos núcleos como o dos elétrons, bem como a interação entre todos os corpos. Assim, o hamiltoniano completo é dado por

$H={\hat {T_{N}}}+{\hat {T_{e}}}+{\hat {V_{Ne}}}+{\hat {V_{e}}}+{\hat {V_{N}}}$

onde ${\hat {T_{N}}}$ é a energia cinética dos núcleos, ${\hat {T_{e}}}$ a energia cinética dos elétrons, ${\hat {V_{Ne}}}$ a energia de atração elétron-núcleo, ${\hat {V_{e}}}$ a interação repulsiva entre os elétrons e ${\hat {V_{N}}}$ é a energia potencial de repulsão núcleo-núcleo^[1].

Ao considerar esse hamiltoniano, a equação de Schrödinger para um sistema de muitos corpos não possui solução analítica e aproximações são necessárias. A primeira aproximação é a de Born-Oppenheimer que desacopla o movimento dos elétrons ao dos núcleos. Essa aproximação é razoável, já que a massa dos núcleos é muito maior que a dos elétrons que se rearranjam rapidamente após qualquer alteração na posição dos núcleos^[4]. Com isso, a energia cinética dos núcleos se torna um termo constante em relação ao movimento dos elétrons, e o hamiltoniano pode ser escrito como

${H}={H}_{ele}+{\hat {V}}_{N}$

onde

${H}_{ele}={\hat {T}}_{e}+{\hat {V}}_{Ne}+{\hat {V}}_{e}$

é denominado hamiltoniano eletrônico. A equação de Schrödinger para todos os elétrons do sistema é

${H}_{ele}\psi _{e}=E\psi _{e}$

onde $\psi _{e}$ é a função de onda total do sistema eletrônico e $E$ é a energia.

Teoremas de Hohenberg e Kohn

A Teoria do Funcional da Densidade está embasada em dois teoremas propostos por P. Hohenberg e W. Kohn (HK)^[5] em 1964. Os teoremas são válidos para um sistema constituído por um número arbitrário de elétrons confinados numa caixa, sujeitos a um potencial externo $v(\mathbf {r} )$ e à repulsão coulombiana mútua.

1º Teorema: O potencial externo $v(\mathbf {r} )$ sentido pelos elétrons é um funcional único da densidade eletrônica $n(\mathbf {r} )$ .

A prova deste teorema é feita por reductio ad absurdum. Considerando o hamiltoniano eletrônico $H_{ele}$

$H_{ele}=T+U+V$

onde a energia cinética total $T$ , a energia potencial proveniente do potencial externo $V$ e a repulsão coulombiana $U$ são dados por

$T={\frac {1}{2}}\int {\nabla \psi ^{*}(\mathbf {r} )\nabla \psi (\mathbf {r} )d\mathbf {r} }$

$V=\int {v(\mathbf {r} )\psi ^{*}(\mathbf {r} )\psi (\mathbf {r} )d\mathbf {r} }$

$U={\frac {1}{2}}\int {{\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\psi ^{*}(\mathbf {r} )\psi (\mathbf {r} ')\psi (\mathbf {r} ')\psi (\mathbf {r} )d\mathbf {r} d\mathbf {r} '}$

Por simplicidade, supõe-se que o estado fundamental é não degenerado e a densidade eletrônica nesse estado é dada por

$n(\mathbf {r} )=\int {\Psi ^{*}(\mathbf {r} )\Psi (\mathbf {r} )d\mathbf {r} }$

Agora, suponha que outro potencial $v'(\mathbf {r} )$ , associado ao hamiltoniano $H'_{ele}$

$H'_{ele}=T+V'+U$

com estado fundamental $\Psi '$ e energia $E'$ , dê origem a mesma densidade $n(\mathbf {r} )$ .

Para $\Psi$ ser diferente de $\Psi '$ , $v'(\mathbf {r} )-v(\mathbf {r} )$ necessariamente não é uma constante e as funções de onda satisfazem diferentes equações de Schrödinger. Pelo princípio variacional, a energia do estado fundamental é mínima para função de onda exata daquele estado, de forma que as desigualdades abaixo são válidas.

$E'=\langle \Psi '|H'_{ele}|\Psi '\rangle <\langle \Psi |H'_{ele}|\Psi \rangle =\langle \Psi |H_{ele}+V'-V|\Psi \rangle$

$E'<E+\int {[v'(\mathbf {r} )-v(\mathbf {r} )]n(\mathbf {r} )d\mathbf {r} }$

$E<E'+\int {[v(\mathbf {r} )-v'(\mathbf {r} )]n(\mathbf {r} )d\mathbf {r} }$

Ao somar as duas desigualdades obtém-se:

$E'+E<E+E'$

que é uma inconsistência. Dessa forma, assumir que a densidade é igual para $v'(\mathbf {r} )\neq v(\mathbf {r} )$ gera um absurdo decorrente de $\Psi$ ser necessariamente diferente de $\Psi '$ . Conclui-se que a unicidade de $n(\mathbf {r} )$ exige que $\Psi =\Psi '$ e $v'(\mathbf {r} )-v(\mathbf {r} )$ seja constante, portanto, o potencial externo é um funcional único da densidade eletrônica.

O 1º teorema de HK demonstra que a densidade pode ser a variável fundamental na determinação da estrutura eletrônica e isso é sumarizado pela sequência abaixo

$n(\mathbf {r} )\Rightarrow \Psi \Rightarrow v(\mathbf {r} )\Rightarrow {\text{Observáveis}}$

onde o conhecimento da densidade eletrônica implica no conhecimento da função de onda e do potencial externo que determina o hamiltoniano do sistema e, consequentemente, todos os observáveis no estado fundamental.

2º Teorema: A energia do estado fundamental é mínima para densidade $n(\mathbf {r} )$ exata.

O segundo teorema expressa que a energia do estado fundamental é um funcional da densidade eletrônica cujo valor mínimo é obtido para densidade exata. Para provar esse teorema, considere o funcional

$E_{v}[n(\mathbf {r} )]\equiv \int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+F[n(\mathbf {r} )]$

onde

$F[n(\mathbf {r} )]=\langle \Psi |T+U|\Psi \rangle$

é denominado funcional universal. Do método variacional, o funcional $\epsilon _{v}$ da função de onda $\Psi '$

$\epsilon _{v}[\Psi ']=\langle \Psi '|V|\Psi '\rangle +\langle \Psi '|T+U|\Psi '\rangle$

é mínimo para o estado fundamental $\Psi$ . Se $\Psi '$ for o estado fundamental associado ao potencial externo $v'(\mathbf {r} )$ , a seguinte relação é válida

$\epsilon _{v}[\Psi ']=\int {v(\mathbf {r} )n'(\mathbf {r} )d\mathbf {r} }+F[n'(\mathbf {r} )]>\epsilon [\Psi ]=\int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+F[n(\mathbf {r} )]$

de forma que

$\epsilon [n'(\mathbf {r} )]>\epsilon [n(\mathbf {r} )]$

como se queria demonstrar. Em linhas gerais, o segundo teorema de HK apresenta um critério para determinar a densidade do estado fundamental.

Se $F[n(\mathbf {r} )]$ for um funcional conhecido, o problema de determinar a densidade e energia do estado fundamental de um sistema eletrônico em dado potencial externo se reduz a minimização do funcional $E_{v}[n]$ . Como as interações de Coulomb são de longo alcance, é conveniente separar essa interação do funcional universal

$F[n]={\frac {1}{2}}\int {{\frac {n(\mathbf {r} )n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} d\mathbf {r} '}+G[n]$

e definir o funcional $G[n]$ que deve estar relacionado às energias cinética, de troca e correlação dos elétrons. Apesar da aproximação de Born-Oppenheimer, o desenvolvimento da teoria é exato até esse ponto, entretanto, não é conhecida nenhuma forma analítica para o funcional $G[n]$ e aproximações devem ser tomadas para que seja possível determinar a densidade eletrônica do estado fundamental.

Equações de Kohn-Sham

W. Kohn e L. J. Sham (1965)^[6] foram os primeiros a apresentar uma tática para determinar a estrutura eletrônica de sistemas com muitos elétrons a partir da minimização do funcional $E_{v}$ .

O ansatz de Kohn-Sham propõe que a densidade do estado fundamental de um sistema com elétrons interagentes seja igual à densidade do estado fundamental de um sistema fictício com elétrons não interagentes em um potencial efetivo, de forma que o funcional universal $G[n]$ é dado por

$G[n]\equiv T_{s}[n]+E_{xc}[n]$

onde $T_{s}[n]$ é a energia cinética do sistema não interagente com densidade $n(\mathbf {r} )$ e $E_{xc}[n]$ é a energia de troca e correlação de um sistema interagente de mesma densidade $n(\mathbf {r} )$ . Com isso, o funcional de energia que deve ser minimizado é

$E_{v}[n]=\int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+{\frac {1}{2}}\int {{\frac {n(\mathbf {r} )n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} d\mathbf {r} '}+T_{s}[n]+\int {n(\mathbf {r} )E_{xc}[n(\mathbf {r} )]d\mathbf {r} }$

A resolução do problema de muitos corpos esbarra num funcional com fórmula analítica não conhecida $E_{xc}[n]$ e, posteriormente, será necessário aproximar esse termo.

A densidade eletrônica exata é um extremo do funcional de energia $E_{v}$ e a carga eletrônica total do sistema de $N$ elétrons é fixa, de forma que a equação abaixo é um vínculo

$\int {n(\mathbf {r} )d\mathbf {r} }=N$

De acordo com o método variacional, incluindo esse vínculo, deve-se ter

$\int {\delta n(\mathbf {r} ){\bigg (}{\frac {\delta T_{s}}{\delta n}}+v(\mathbf {r} )+\int {{\frac {n(\mathbf {r'} )}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} '}+v_{xc}[n]-\mu {\bigg )}d\mathbf {r} }=0$

onde $\mu$ é o multiplicador de Lagrange e $v_{xc}[n]={\frac {\delta E_{xc}}{\delta n}}$ é o potencial de troca e correlação.

A energia cinética do sistema fictício não interagente, em unidades atômicas, é

$T_{s}[n]=-{\frac {1}{2}}\sum _{i}\int {\psi _{i}^{*}\nabla ^{2}\psi _{i}d^{3}r}$

e do ansatz de KS decorre que

$n(\mathbf {r} )=\sum _{i=1}^{N}|\psi _{i}(\mathbf {r} )|^{2}$

é a densidade do estado fundamental.

A solução da equação de minimização que deve resultar em $n(\mathbf {r} )$ pode ser obtida da equação de Schrödinger de uma partícula, já que no sistema fictício os elétrons não interagem

${\hat {h}}^{KS}\psi _{i}(\mathbf {r} )={\bigg (}-{\frac {1}{2}}\nabla ^{2}+v^{KS}[n]{\bigg )}\psi _{i}(\mathbf {r} )=\epsilon _{i}\psi _{i}(\mathbf {r} )$ .

Essa equação é denominada equação de Kohn-Sham, ${\hat {h}}^{KS}$ é o hamiltoniano de KS e

$v^{KS}=v(\mathbf {r} )+\int {{\frac {n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} '}+v_{xc}[n]$

é o potencial efetivo de Kohn-Sham. Normalmente, $\psi _{i}$ são ditos orbitais de KS e é importante destacar que esses orbitais não são as funções de onda do sistema interagente, tal como $\epsilon _{i}$ não é autovalor de energia do sistema real; apenas a densidade do estado fundamental $n(\mathbf {r} )$ é igual nos sistemas real e fictício.

É necessário resolver a equação de KS para determinar a densidade eletrônica, entretanto, $v^{KS}$ depende de $n(\mathbf {r} )$ e não é possível resolver a equação diretamente. Nesse caso, comumente, é adotado um cálculo autoconsistente.

Método de cálculo autoconsistente

Cálculo autoconsistente em DFT

A equação de KS pode ser resolvida através de um cálculo autoconsistente: a partir de uma densidade inicial $n^{j}$ , calcula-se o potencial efetivo de Kohn-Sham $v^{KS}(\mathbf {r} )$ e determinam-se as funções de onda $\psi _{i}(\mathbf {r} )$ pela solução da equação de KS. Em seguida, calcula-se a densidade do estado fundamental $n^{j+1}$ a partir desses orbitais e compara-se com a densidade inicial: se $n^{j+1}=n^{j}$ , diz-se que o cálculo convergiu e a densidade $n^{j+1}$ pode ser utilizada para determinar os observáveis físicos; caso contrário, $n^{j+1}$ é utilizado para calcular o potencial efetivo, o ciclo de autoconsistência é reiniciado e esse processo continua até o cálculo convergir.

A densidade eletrônica inicial é arbitrária e, normalmente, é uma distribuição aleatória. Note que para calcular o potencial efetivo de KS é preciso, a priori, aproximar o funcional de troca e correlação $E_{xc}$ , portanto, para iniciar o cálculo autoconsistente devem ser feitas, inicialmente, duas escolhas: densidade eletrônica inicial e a forma de $E_{xc}$ .

Funcionais de Troca e Correlação

A escolha do funcional de troca e correlação é um fator decisivo para o precisão da DFT e um dos aspectos mais atraentes dessa teoria é que mesmo as aproximações mais simples para esse funcional podem fornecer resultados precisos. As aproximações para $E_{xc}$ podem ser separadas em: funcionais locais (como TF, LDA e LSDA onde esse último inclui a polarização de spin), funcionais dependentes do gradiente (GEA e GGA) e funcionais não locais (híbridos DFT, meta-GGA e EXX, etc).

LDA

Na aproximação LDA (do inglês, Local Density Approximation), supõe-se que a energia de troca e correlação de um sistema inomogêneo de densidade $n(\mathbf {r} )$ no ponto $r$ é igual à energia de troca e correlação de um gás de elétrons homogêneo com a mesma densidade. O funcional $E_{xc}$ , para um sistema sem polarização de spin, é escrito como

$E_{xc}^{LDA}[n]=\int {n(\mathbf {r} )\epsilon _{xc}(n(\mathbf {r} ))d\mathbf {r} }$

onde $\epsilon _{xc}(n)$ é a energia de troca e correlação por elétron do gás de densidade constante $n(\mathbf {r} )$ . Com isso, o potencial de troca e correlação

$v_{xc}[n]={\frac {\delta E_{xc}}{\delta n}}={\frac {d}{dn(\mathbf {r} )}}{\big [}n(\mathbf {r} )\epsilon _{xc}(n(\mathbf {r} )){\big ]}$

depende apenas da densidade no ponto $\mathbf {r}$ .

A energia de troca e correlação por elétron é decomposta linearmente nessas interações, de forma que

$E_{xc}\approx E_{xc}^{LDA}[n]=\int {n(\mathbf {r} )[\epsilon _{x}(n(\mathbf {r} ))+\epsilon _{c}(n(\mathbf {r} ))]d\mathbf {r} }$

onde energia de troca $\epsilon _{x}$ do gás homogêneo é conhecida analiticamente^[7] e a energia de correlação $\epsilon _{c}$ deve ser parametrizada ou determinada através de outras simulações computacionais.

D. M. Ceperley e B. J. Alder (1980) determinaram $\epsilon _{c}$ com grande precisão para certos valores de densidade a partir de uma simulação com Monte Carlo Quântico para o gás homogêneo e interagente^[8]. A partir desses valores, J. Perdew e A. Zunger (1981) propuseram uma parametrização para $\epsilon _{xc}$ conhecido como LDA-PZ^[9]. Por muitos anos, a aproximação LDA foi utilizada no cálculo de estruturas de banda e energia total já que apresenta bons resultados mesmo para sistemas com densidade não uniforme e isso se deve a um cancelamento sistemático: a energia de correlação é subestimada, enquanto a de troca é superestimada^[10].

GGA

Se a densidade eletrônica for não uniforme, a aproximação LDA não descreve bem os sistemas reais que são inomogêneos, já que os elétrons estão sujeitos a variação espacial do campo elétrico dos núcleos e se repelem mutuamente. Nesse contexto, surge a aproximação GGA (do inglês, Generalized Gradient Approximation) que considera a variação espacial da densidade $n(\mathbf {r} )$ ao propor que o funcional de troca e correlação seja expresso em termos de $n(\mathbf {r} )$ e $\nabla n(\mathbf {r} )$ . Genericamente:

$E_{xc}\approx E_{xc}^{GGA}[n]=\int {f{\big (}n(\mathbf {r} ),\nabla n(\mathbf {r} ){\big )}d\mathbf {r} }$ .

Existem várias escolhas para a função $f$ e isso implica em diferentes aproximações GGA, como os funcionais PBE (proposto por J. P. Perdew, Kieron Burke e Matthias Ernzerhof em 1996^[11]) e BLYP (que combina o funcional de troca proposto por A. D. Becke (1988)^[12] com o funcional de correlação formulado no mesmo ano por C. Lee, W. Yang e R. Parr^[13]). As aproximações GGA descrevem bem as ligações químicas, mas falham na descrição de interações fracas como as forças de van der Waals.

Pesquisar este blog

MECÂNICA GENERALIZADA GRACELI - QUÂNTICA QUÍMICA RELATIVISTA [14]

Explanação

Materiais cristalinos

Introdução

Contexto geral

Contexto avançado

Ilustração do conceito para compartimento monodimensional quadrado

O caso tridimensional

Energias de Fermi típicas

Anãs brancas

Núcleos

Explanação

Materiais cristalinos

Visão geral

Formalismo

Equação de Schrödinger

Aproximação de Born-Oppenheimer

Teoremas de Hohenberg e Kohn

Equações de Kohn-Sham

Método de cálculo autoconsistente

Funcionais de Troca e Correlação

LDA

GGA

Comentários

Postar um comentário

Postagens mais visitadas deste blog